The Risk Parity Gorilla in the Room

The Invisible Gorilla

About 12 or 13 years ago, I was invited to a talk given by the famous Mathematics Professor and billionaire founder of Renaissance Technologies, James Simons. He gave a fascinating discussion of his career, the importance of luck, even for someone as brilliant as him (my phrasing), and why one should not become too obsessed with one’s goals if it gets in the way of current success. At some point he told the audience that he was going to show us a 2-minute film to “test our concentration”. The famous multi-billionaire Hedge Fund creator and Veblen Prize winner in Geometry was challenging his audience to concentrate. What a set up.

He told us the film would have a group of six people with 3 basketballs. Our task was to simply count the number of times the basketballs were passed. The lights went out, the film comes on and I focused as much as possible on the passers. There were 3 males and 3 females, and they were in constant motion while randomly passing the basketballs to each other. It was very difficult to count the passes and did require great concentration. The film ends quickly and the lights in the auditorium come back on. He lets us wait about 20 seconds and then asked, “how many counted 38?” About 10-15% of the audience raised their hand. He congratulated those who got it right. Then he asked, “how many of you saw the man in the gorilla suit?”. I recall only 2 people raising their hand. “What?”.

He then proceeds to tell the audience that a man in a gorilla suit walked slowly into the middle of the group of passers, stopped to look at the camera, waved his hands several times over his head, slowly lowered his hands, and then sauntered out of the picture just before the passers stopped their activity.

I absolutely believed he was playing a trick on the audience. There was no way I thought a man in a gorilla suit was in that film. It was impossible. The group became a bit noisy as we wondered what was going on. He then tells us he would replay the film. When he did, I was genuinely shocked; all I could see was the man in the gorilla suit. I immediately told my colleague “no way is that the same film - that’s the trick - seeing if we will believe anything told us by an authoritative figure regardless of the evidence”.

He then told us the background of the film. Professor David Simons of the University of Illinois (no relation to James Simons) had created the film in 2004. It was called “the Invisible Gorilla” (later a book was written by David Simons in 2010 with the same name). The film is currently on YouTube with 10 million views -- but if you are reading this you will see the gorilla. To this day that “trick” still astounds me. The “obvious” is often lurking just beyond our awareness. Simons’ comment about “testing our concentration” was a classic case of “perception framing”, (term coined by Tversky and Kahneman - “The Framing of Decisions and the Psychology of Choice” -1981). By intensely concentrating on what we were told was the point of the exercise, we were deceived as to what was the real point of the exercise -- and failed miserably.

The Man in the Gorilla Suit -- the 50/50 Risk Parity Portfolio

We call the two-asset class “50/50” risk weighted portfolio of Equities and Fixed Income (i.e., the two-asset class Risk Parity Portfolio) the “Man in the Gorilla Suit”. It is the most obvious portfolio investment that all have missed - certainly we have - and it has consistently outperformed what virtually all institutions have achieved. We missed it because we have instead followed the “perception framing” authoritative figures have told us to use. However, this became egregious when we simultaneously ignored more important issues. In very simple terms, we ignored the most basic rules of portfolio construction that all of us have learned in finance courses, or early in our careers - i.e., the critical role of proper diversification, and the role of the “Tangency Portfolio” along the efficient frontier.

Risk Parity (dollar weights of portfolio constituents change through time inversely with the constituents’ expected volatility) is a concept which has existed since at least the early 1980s, although under different names. A “50/50” Risk Weighted Portfolio, i.e., Risk Parity, allocates “constant risk” (also called “target volatility”) equally to Equities and Treasuries / Fixed income, while also targeting volatility for the whole portfolio.  Portfolio hedging techniques, designed to neutralize risk between two or more asset classes, go back to at least the earliest days of the over the counter derivatives markets - and maybe well before that.

Today, the term “Risk Parity” usually refers to a specific investment strategy that incorporates Equities, Treasuries (and/or other fixed income), and some combination of Commodities and/or TIPs. MSR Indices LLC, in partnership with S&P Dow Jones, helped create their family of Risk Parity Indices (see S&P Dow Jones “Introducing the S&P Risk Parity Indices”). This index applies equal risk weighting, not dollar weighting, to 3 major global asset classes: Equities, Government Notes, and Commodities.

The S&P Risk Parity Indices’ purpose is to perform well in all environments, rather than predict when the next change in economic environments will arise. It is designed to do well when there is rising growth, declining growth, rising inflation, and declining inflation. S&P Dow Jones has created a recent PowerPoint presentation (“A Passive Approach to Risk Parity” -- Rupert Watts, May 2019) which describes how and why Risk Parity should perform well in different economic regimes.

This paper, however, will focus on the “50/50” Risk Parity portfolio of stocks and bonds, as they are the core asset classes of all investor portfolios. We will compare it with pension fund performance and with the very familiar 60/40 strategy. We will provide evidence for the last 30+ years that Pension Funds performed very close to the traditional, albeit stylized, dollar weighted 60/40 portfolio of the S&P 500 and the 10-year Treasury (while also slightly under-performing), despite almost herculean efforts by these same Pension Funds to diversify away from 60/40 (by “stylized” we mean a representative subset of an investment style).

Interestingly, particularly for those familiar with Modern Portfolio Theory (MPT), the 50/50 Risk Parity portfolio’s market cap weighting has been much closer to the US Capital Weighted Market Portfolio (the “Market Portfolio”) of stocks and bonds than 60/40. A Risk Parity portfolio of US Stocks and Treasuries has also outperformed 60/40 in absolute and risk-adjusted terms, hypothetically, since 1926 (Asness, Frazzini and Pedersen - "Leverage Aversion and Risk Parity, May draft 2011 --Table 2 footnote”). We believe that 50/50 Risk Parity provides superior performance because it provides a return that is much closer to MPT’s Tangency Portfolio – a portfolio that MPT tells us cannot be beaten in the long-run. Our analysis of Risk Parity will use the 10-year Treasury and the S&P 500; the point is to explain the concept as easily as possible. But 50/50 Risk Parity is as or more effective when combining a broader array of high-grade fixed income instruments with a broader array of Equity instruments. It is truly “the gorilla” that no one has seen.

50/50 Risk Parity is the Best Market Benchmark Portfolio for Stocks and Bonds

The size of the US Fixed Income Market was approximately $43 Trillion as of 2018. The capitalization of the NYSE and NASDAQ was $30 Trillion (U.S. Companies only). Globally, the Equity and Bond markets, respectively, were $75 Trillion and $103 Trillion, also as of 2018. US Fixed Income publicly traded securities include Treasuries, MBS, Agencies, Corporates and Municipals. Closely held shares, preferred stock and US owned equities of foreign companies total another $12 trillion (source for Market Data: SIFMA “Capital Markets Factbook”).

As of 2018, Fixed Income was approximately 60% of the public securities outstanding in the United States versus 40% Equities. Globally, Fixed Income was 58% and Equities 42%. This ratio obviously changes over time, primarily because debt grows at a slow steady pace and the Equity market’s value grows at a volatile and unsteady pace. The Market Portfolio, defined in terms of asset classes, should have these percentages of Equity and Fixed Income.

Bond Markets have always been larger than the Equity Markets. For example, from 1978-2018, the US Fixed Income market generally ranged in weighting from approximately 60% to 70% of total market capitalization (source: Federal Reserve Bank of St. Louis). While this is well known, it is rare to see the Market Portfolio mentioned as having had a better Sharpe ratio (as predicted by MPT) than the portfolios that are generally constructed by the largest Pension funds and many investment advisors, but it has.

Fixed Income is generally owned in larger percentages by a certain class of investors, for example Insurance Companies and Banks. Equities are generally owned in larger percentages by Pension Funds and Individuals. The latter generally construct portfolios that approximate the ubiquitous 60/40 strategy (60% equities and 40% fixed income) and often higher equity weighted portfolios. The strong popularity of high equity weighted portfolios among the largest Pension Funds and individuals has made 60/40 almost a de facto investor benchmark, along with the S&P 500.

One reason this is interesting is that a “50/50” Risk Parity portfolio of “large cap” equities, equivalent to the S&P 500, and the 10-year Treasury has had a dollar weighted average through time of 65% Treasuries and 35% equities from 01/01/1973 - 7/31/2019 (source: Portfolio Visualizer.com). In other words, our admittedly “stylized” Risk Parity portfolio, which is highly liquid and easily implemented, has had average dollar weights comparable to what the US Capital Market Weighted Portfolio of Equities and Fixed Income has been on average since at least 1978.

The Risk Parity portfolio is not the Market Portfolio of Stocks and Bonds, but it comes as close as one can get, ex-ante (or expected), to the highest ex-post (or actual) Sharpe ratio portfolio that combines these two asset classes. The reason is straight forward: Modern Portfolio Theory tells us that the expected long-term Sharpe ratio of these two asset classes should be approximately equal, and historical data supports this (sources: “Risk and Return of Different Asset Allocations” — Norges Bank; “Asset Allocation by the Book” -- J.P. Morgan Asset Management).

The J. P. Morgan study uses data from 1926-2011 and is sourced from Ibbotson Associates. It measures the Sharpe ratio of US Government Bonds and US Equities at .43 and .40, respectively, with a long-term correlation between the two asset classes of .08. Norges Bank’s data is from 1961-2016 and measures the respective Sharpe ratios of US Government bonds and the S&P 500 at .34 and .38. The highest expected Sharpe ratio of a portfolio of any “two asset classes” will always be one that allocates risk equally when the two assets have the same expected Sharpe ratios (for more detailed analysis on Risk Parity as the implementable version of MPT see “Risk Parity for the Long Run” by Partridge and Croce in Alternative Investment Analyst Review).

Additionally, from 1945-2018, there were 16 calendar years when the S&P 500 was down (average annual loss of 11.7%). In 15 of those years, the 5-year Treasury had positive returns (average annual gain of 6.2%). Additionally, Treasuries and Stocks have not been down in the same year since 1969. While the long-term correlations of these two asset classes are slightly above zero, there is much evidence that there is some conditional negative correlation between them.

Efficient Frontier and the Tangency Portfolio

A brief update on some terminology will be helpful. These are simple and intuitive descriptions for a two-asset class portfolio, the topic of this paper.

The “Efficient Frontier”, for two asset classes, is simply a graph of returns and volatility that is drawn based on all possible dollar combinations of the two asset classes. In our two-asset class example, at one extreme is 100% Equities and, at the other, 100% 10-year Treasuries. In the middle is every combination in between (e.g., 90/10, 80/20…20/80, 10/90, etc.). Such graphs are typically drawn with Portfolio Volatility on the X-axis and Portfolio Returns on the Y-axis. It is called “efficient” because for any specific level of volatility there is only one combination which can produce the highest rate of return for that volatility.

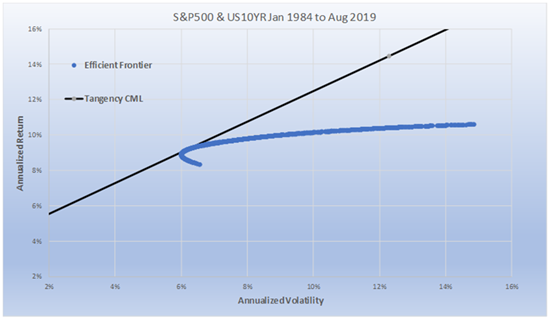
The Tangency Portfolio is the point on the Efficient Frontier that has the highest Sharpe ratio versus all other combinations of weightings (i.e. portfolios) on the Efficient Frontier. It is called the “Tangency Portfolio”, because one can draw a straight line (called the “Capital Market Line”, or “CML”) that is “tangent” to that point on the Efficient Frontier, and all other points on the Efficient Frontier fall below the line. The Capital Market Line represents the returns and volatilities (annualized standard deviations) of different leverage levels of the Tangency Portfolio. Chart 1 is an illustration of this. At the Tangency point, the portfolio has no leverage. Above the Tangency point, the portfolio is leveraged, or “borrows” to own more of the portfolio. Below the Tangency point, the portfolio replaces part of the Tangency Portfolio with “cash”, or “lends” to own less of the portfolio.

Chart 1: 

Risk Parity and the Tangency Portfolio

Since 1984, the ex-post, or “after the fact”, Tangency Portfolio (of the two “assets” - the S&P 500 and the 10-Year Treasury) had a notional weighting of 75% 10-Year Treasury and 25% S&P 500. The average notional weighting for this 36-year period for the Risk Parity portfolio was 70% 10-Year Treasury and 30% S&P 500. From 1974 to 2019, the ex-post Tangency portfolio weighting of the US Total Stock Market and the Long-Term Corporate Bond market had virtually the exact weighting of Risk Parity’s average weighting (35% Equities and 65% Bonds). We wonder how many investors were aware that the highest Sharpe ratio portfolio had that much Fixed Income. However, there is one major problem with the Tangency Portfolio - one cannot invest in it.

The reason is it was not known until after the fact. One could have invested in Risk Parity, however. And Risk Parity will almost always be very similar to the ex-post Tangency Portfolio over long periods of time. Chart 2 shows that the Risk Parity portfolio sits right near the Tangency Portfolio on the Efficient Frontier (from 1984-2019). Furthermore, the 50/50 Risk Parity CML line, drawn for different levels of volatility just like the Tangency CML, sits just below the Tangency Portfolio CML. The Tangency Portfolio and CML are “after the fact” fixed weightings and, to repeat, cannot be known in advance. Therefore, it cannot be implemented. The Sharpe ratio for the (unattainable) Tangency Portfolio was .85, while the easily implementable 50/50 Risk Parity Strategy was a very close .83.

This is not as surprising as it might first appear. First, there is a range of weightings where the Sharpe ratios of the two portfolios are almost the same. Secondly, Risk Parity is trying to equally risk weight two low correlated (on average) assets of Treasuries and Equities which have similar expected long-term Sharpe ratios.  In fact, it would be very surprising if the long-term ex-post Tangency Portfolio had a materially different Sharpe ratio than Risk Parity.

Chart 2

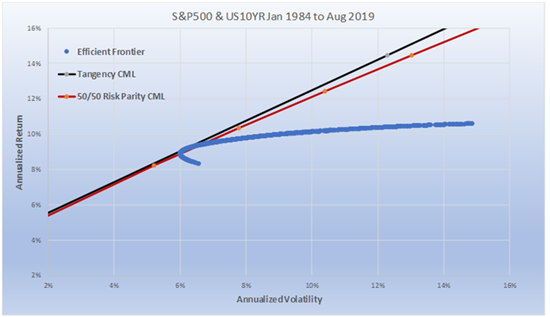
Many critics of Risk Parity have pointed out that Sharpe ratios are sub-optimal in any portfolio when one is risk weighting asset classes with materially different Sharpe ratios. We completely agree. Furthermore, for shorter time frames we  expect the Tangency Portfolio (i.e., the highest Sharpe ratio portfolio for the chosen time period) to be very different than the Risk Parity portfolio (or any other portfolio weighting) as equities and fixed income perform differently from each other during these shorter time frames.  For example, the 5-year Tangency Portfolio from 2000-2004 consisted of a 100% weighting to the 10-year Treasury. No amount of Equity could have been added to the portfolio to improve the Sharpe ratio. And, it would have taken an omniscient investor to have known that would be the optimal portfolio weighting on the eve before the millennium.

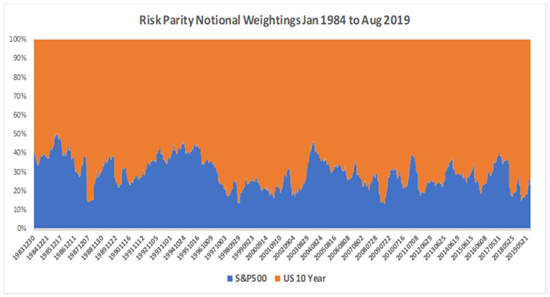
Keep in mind, that for any time period, the Tangency Portfolio, by definition, will always have the highest Sharpe ratio - and it will be impossible to know what that is in advance. To state the obvious, there will always be a Tangency portfolio for every time frame - from 1 day to 100 years - that will be better than whatever any investor does. Sometimes the Tangency portfolio will even be 60/40, and sometimes it will be Risk Parity’s average weighting. But the challenge is to achieve as close as possible to the ex-post Tangency Portfolio, given that we do not know what it is in advance. As time expands, Risk Parity’s risk adjusted returns will almost always come increasingly closer to the Tangency portfolio for that time frame. Chart 3 shows that notional weightings between the two asset classes change through time within a Risk Parity portfolio. The notional weightings change as a result of the comparative volatility of each asset class changing over time. The objective is to maintain equal risk, and as volatility changes equal risk will result in different notional weightings.

Chart 3

Risk Parity and The Impact of Volatility Skew

(For a brief intuitive summary of Volatility Skew please see “Learn About Volatility Skew” at thebalance.com).  As previously noted, the average notional or nominal weightings of the Risk Parity portfolio above in Chart 3 was 30/70 compared to the Tangency portfolio’s weighting of 25/75. Given that one is a “fixed nominal weighting” scheme and the other a “floating nominal weighting” (although fixed risk-weighted) scheme, it might seem surprising that the nominal weightings are so close.

There are good reasons for this. The authors, Partridge and Croce (referenced earlier), use the time period from 1958 to 2011 to demonstrate, in part, why this is the case. In the short run, the Tangency portfolio will almost always be different than the Risk Parity portfolio. But in the long run Risk Parity weighting approaches the Tangency portfolio as the relative volatility declines or rises between the two asset classes. The relative weightings of a given asset will increase (as volatility declines more in that asset) or decrease (as volatility rises more in that asset). They make the point that declining volatility is generally associated with rising returns and vice versa. This implies that the risk weightings tend to move toward the higher long-term risk adjusted portfolio. We hypothesize a rationale for why this occurs.

We hypothesize that the volatility skew in the equity market strongly influences the notional weightings in both two-asset class Risk Parity and Tangency portfolios. In the Tangency portfolio, the simple increase in equity values (often when equity volatility declines) will cause its relative weighting to rise. A simple decrease in equity values (often when volatility rises) will cause its relative weighting to fall. The reasons relative weightings change in Risk Parity are a little more complex.

The changes in weightings within a Risk Parity portfolio are purely a function of changes in realized volatility. This benefits Risk Parity. The reason is two-fold. First, volatility tends to cluster, or exhibit positive serial correlation (i.e., large changes tend to be followed by large changes…and small changes tend to be followed by small changes) as was first observed by Benoit Mandelbrot in the 1960s (see “Overview of Volatility Clustering”. Mike Moffat. ThoughtCo). This means that sizing of Equities within a Risk Parity portfolio, relative to changes in volatility, also clusters and is not random.

Secondly, it has been shown, empirically, that there is a negative correlation between realized volatility in Equity markets and Equity returns. Crestmont Research has studied monthly and annual data from 1962-2018 (“Relationship of Volatility & Market Returns”) of the S&P 500. They create quartiles of realized volatility, from low to high. On a monthly basis, there is a direct correlation between returns and realized volatility. The highest quartile volatility has an expected monthly loss of 70 basis points versus a 1.7% gain in the lowest volatility quartile. The higher the volatility observed, the lower is the expected return. When observing volatility on an annual basis, the upper quartile volatility years have an expected loss of minus 5%, while the lowest quartile years have an expected gain of 13.4%. These are not predictive but contemporaneous. This benefits Risk Parity as it adjusts weightings according to contemporaneous measures of volatility. It weights Equity less when returns are expected to be lower, and weights Equity more when returns are expected to be higher.

The authors Papageorgiou, Reeves, and Sherris in their paper “Equity Investing with Targeted Constant Volatility Exposure” demonstrated that from 1929-2013 a constant volatility Equity portfolio (such as used in Risk Parity) had an information ratio of .65 versus .51 for a normal dollar weighted portfolio of the S&P 500. Perchet, Corvalho, Heckel, and Moulin in “Predicting the Success of Volatility Targeting Strategies” explain how volatility clustering and the negative correlation between volatility and returns creates higher risk-adjusted returns for the equity portfolio.

The relative weightings in a Risk Parity Portfolio are driven by the changes in volatility in both the Equity and Fixed Income markets. However, it is the realized volatility in the Equity markets which has the greater impact. Its volatility is inversely related to returns (as well as position sizing). Fixed Income, on the other hand, while having a long term zero correlation with equities and demonstrating some conditional negative correlation (for example, during “flights to quality”) does not exhibit persistent volatility changes that are correlated to returns. On average, its change in weighting, due to changes in volatility, has neither a positive nor a negative impact on Risk Parity in the long run.

In the long run, therefore, the notional weightings in the Risk Parity portfolio mimic the notional weightings of the Market Portfolio (and, therefore, in the long run the Tangency Portfolio). Equity weightings rise relative to fixed income when equity prices rise in the Market Portfolio simply because of the higher prices, and the same occurs in the Risk Parity portfolio because volatility is typically declining at the same time. The opposite also occurs when equity prices fall and volatility increases.

“Counting Passes”: Pension Fund Data, “60/40” and the Paradox of Alternatives

The most traditional investment strategy, and the one that is most correlated to long term return results of Pension Funds, is the ubiquitous 60/40 strategy. According to Cliffwater LLC, 70% of State pension assets were invested in equities and fixed income with a ratio of “70/30” -- 70 percent equities and 30 percent fixed income. (see Cliffwater- “An Examination of State Pension Performance, 2000-2018”). On average, they invest 70% of their assets in public securities using a 70/30 split. As of 2018, according to Cliffwater, the remaining 30% of total assets of Pension Funds were in alternatives, increasing from 10% in 2006.

NASRA estimates that in 2018 there was a 68/32 split for those assets invested in public markets, which they derive from their latest “Public Fund Survey”. The Pew Research Center (“State Public Pension Funds Practices and Performance -2016 Data Update”) estimates a 65/35 allocation for 74% of Pension Fund assets. Pew estimates 26% of Pension assets were in alternatives.

Historically, according to Pew, the mix of Pension Fund assets has had an interesting trend over the last 67 years. In 1952, virtually 100% of assets were in fixed income. 30 years later, 1982, 78% was in fixed income. Now, fixed income has declined to 20% and equity and alternatives are about 80%, virtually the exact opposite ratio of the highest Sharpe ratio portfolio. For those Pension Funds who invest in private equity, they invest almost 10% of their assets on average. For those who invest in hedge funds, they invest 7.7% of their assets on average.

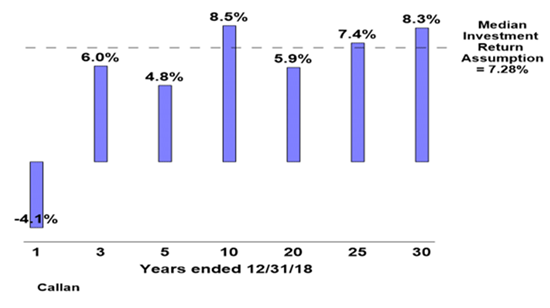
The median Pension fund return - according to Callan Associates referenced in the NASRA paper - measured over 7 different time frames beginning in 1989 and ending 12/31/2018 and shown in Chart 4 - shows that the performance of Pension Funds, collectively, has been remarkably close to our stylized 60/40 returns of the S&P 500 and the 10-Year Treasury, with a .995 correlation for these seven different time frames. It is almost as if 60/40 were the Pension Fund portfolio. We recognize that the overlapping periods increases the correlation, however, returns are very similar to 60/40 for each period, regardless of timeframe.

Pew also quantified the large dispersion of performance for 44 very large State Pension Funds between 2007-2016. Both median performance and average performance were about 5.5%, but the range was between 3.8-6.8%. US 60/40 had virtually the same annualized return (6.71%) as the highest performer for this time frame. Even more sobering is that 50/50 Risk Parity had twice the Sharpe ratio as 60/40 for this same time frame. High dispersion of performance is also a clear indication that it is risky to engage in “out-performance” investing (i.e., the pursuit of alpha). This also gives credence to the idea that markets provide only zero-sum outcomes, (relative to any benchmark). When investors are continually changing their investment profile into high correlated higher fee strategies, we should expect, and do get, these kinds of results.

We call this approach the equivalent of “counting passes” in our Gorilla metaphor. Pension Fund investors, who seek to improve returns, are inadvertently framing their perception to find better returns in non-diversifying alternatives. They have been seeking to outperform by investing in relatively illiquid and opaque investments by replacing fixed income during one of the best fixed income periods in history and by moving away from the portfolio weighting which has the highest expected Sharpe ratio. They have moved consistently into private equities and other alternatives, which underneath it all, are correlated primarily to equities but with higher fee structures. This would be acceptable if institutional performance were better, but evidence shows otherwise. Chart 4 illustrates Pension Fund returns since 1989.

The comparable returns during these periods for 60/40 (S&P 500 and the 10 year) were -2.29%, 5.96%, 6.01%, 9.08%, 5.75%, 8.00%, and 8.93%. 60/40 has outperformed pension funds in 5 of the seven-time frames. As already mentioned, the correlation between Pension Fund returns and 60/40, for these time frames, was .995. Cliffwater also presents Pension fund 18- and 10-year asset weighted returns ending on 6/30/2018 instead of 12/31/2018. The asset weighted 18-year return was 5.87% (the US 60/40 was 5.90%) and the 10-year return was 6.49% (US 60/40 was 7.90%).

Chart 4 – Pension Fund Returns

When one reflects on this, it should cause some alarm. Trillions of dollars, time, and manpower are invested in investigating high fee methods of investing; most specifically in private equities and hedge funds, and the results are questionable.

We do know there are “two free lunches” in the investment world: diversification and low fees. We also know that greater diversification is provided to equities when combined with more risk-free or very high-grade bonds, than with other forms of investments such as private equity, equity hedge funds, low grade debt and emerging markets. This does not preclude including these investments in a portfolio, but an ideal portfolio does require more risk-free or very high-grade fixed income securities, as well as strategies with lower fees. This is the opposite direction institutions have taken.

Comparative Performance of 50/50 Risk Parity versus 60/40 and the Tangency Portfolio

We have demonstrated that the Pension Fund Sector has performed very much like a 60/40 portfolio with slight under-performance. We have also described how and why Risk Parity performs close to the Tangency portfolio and outperforms 60/40. We will now show three Charts in this section for the last 36 years which compares these portfolios.

Chart 5

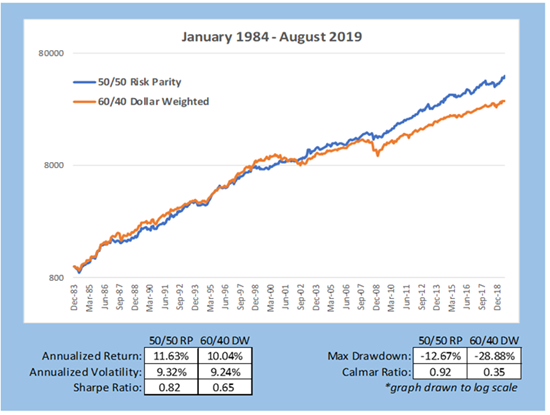
Chart 5 above provides summary statistics and comparative VAMI graphs of 60/40 versus Risk parity. Risk Parity targets the same annualized volatility as the 60/40 portfolio for easier comparative analysis. In a real-world implementation, it is unlikely one would have the same ex-post volatility between these two portfolios. However, one benefit of Risk Parity is the investor chooses the desired risk, not necessarily to match the volatility of 60/40. 60/40 strategies, due to the high risk weighting of equities, has a much higher drawdown, as occurs most of the time versus Risk Parity.

Chart 6 

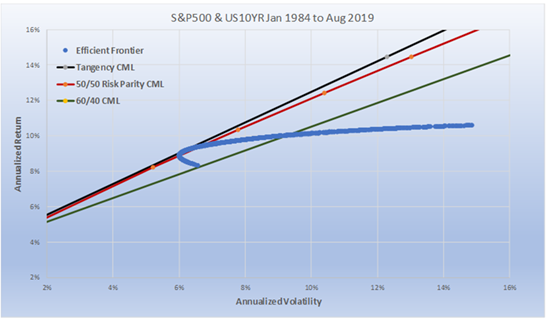
Chart 6 compares the non-investable Tangency Portfolio with Risk Parity and 60/40. What is interesting is the difference in the notional weightings of the 3 different portfolios. As we have tried to drive home in this paper, the highest possible Sharpe ratio portfolio (the non-investable Tangency Portfolio), is very close to the Sharpe ratio and notional weighting of the Risk Parity portfolio (30% equity and .85 Sharpe versus 35% Equity and .82 Sharpe).

60/40, obviously, has 60% equity and from Chart 5 a 0.65 Sharpe ratio. Since the Efficient Frontier (the blue line) captures all relative weightings, it intersects the 60/40 Capital market line as well. Where it crosses matches the results in Chart 5. The efficient frontier, i.e., the blue line, as we described earlier is also unlevered. The unlevered non-investable Tangency Portfolio has a total annualized return of 9.17% and a volatility of 6.16% (where the blue line intersects with the black line). The unlevered portfolio of Risk Parity has 9.20% return and 6.38% volatility (where the blue line intersects with the red line). From Chart 5 we know that 60/40 has an un-levered return of 10.04% with a volatility of 9.24%.

Chart 7

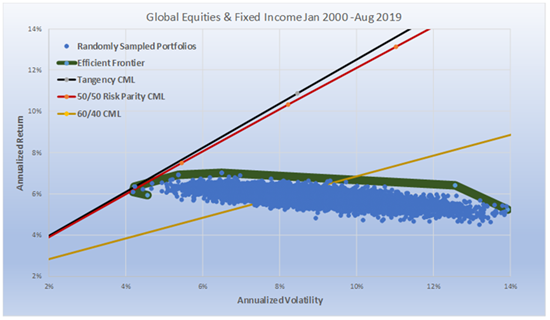
Chart 7 compares a more realistic global portfolio of Stocks and Bonds (we use 13 futures markets: S&P500, Nasdaq 100, Dow Jones Industrials, EuroSTOXX50, FTSE100, DAX, NIKKEI, US5yr, US10yr, US30yr, LONG GILT, BOBL, and BUND), but we only are able to use 20 years of data, as that is as far as the futures data exists. Having said that, the results are consistent with our major hypothesis and the one that should matter most to investors. In the long run, Risk Parity is as close as one can get to the Tangency Portfolio of two asset classes when the expected Sharpe ratios of the two asset classes are similar to each other.

For the ex-post Tangency Portfolio we chose to run a scenario which would result in it getting the highest Sharpe ratio possible. Rather than grouping them in two asset classes we let the “look back” optimizer choose any combination of the 13 contracts. The possible number of combinations is almost infinite; to keep it within reason, we ran 50,000 randomly chosen portfolios.

For Risk Parity, we used our two asset class methodology. We equally risk weighted all equities, all fixed income, and then equally risk weighted the two asset classes and created its CML by running it at a range of target volatilities between 1% and 15%. 60/40 had 60% of its dollars in equal dollar weighted equities, and 40% of its dollars in equal dollar weighted fixed income. The Sharpe ratio of the non-investable Tangency portfolio was 1.04; for Risk Parity it was 1.01 and for 60/40 it was .33. The important thing to recognize is how close RP was to the Tangency Portfolio and not how much it outperformed 60/40. The Bond weightings for the Tangency portfolio was 18%, and for Risk Parity it averaged 20%.

One should find this interesting. One method (the ex-post Tangency Portfolio) simply curve fits the best result when all information is known. The other method uses a walk forward risk weighting approach (that is easily implemented ex-ante). This paper explained why this seemingly non-intuitive relationship really is the expected outcome.

Closing Comments

Institutional investors should be judged by how they perform relative to a Risk Parity portfolio of Equities and Fixed Income. They should also be judged, not just by absolute returns, but by risk-adjusted returns. There is no basis at all for using 60/40 or the S&P 500 for a benchmark as these have little to do with Capital Market weightings, and do not incorporate any coherent framework regarding portfolio theory. 50/50 Risk Parity comes closest to tracking the Tangency Portfolio over the long run and is therefore ideal as a Benchmark.

As I was finishing the final details of this essay, the WSJ announced the estimate of Pension Fund returns for the year ending 06/30/19 was 6.79%. Once again, Pension Funds underperformed Risk Parity for the prior 12 months as we have applied it in this essay. I find this exasperating. We use the “invisible gorilla” metaphor to grab the reader's attention, but its purpose is very serious.

All “models” should be as simple as possible, but not more simple than necessary. Risk parity fits that criteria. We used Large Cap Stocks (S&P 500) and the 10 year Treasury in this study for 2 reasons:

1) we have data for these going back to 1926; and,

2) for the last 30 years, including 6 other subsets of time, it is the 60/40 portfolio of these two instruments which virtually matches the performance of Pension Funds.

Ideally, the reader will think of this as a thought piece. There are many ways to create a Risk Parity portfolio of stocks and bonds. For example, using all the data available, the following is another example of a risk parity portfolio versus 60/40. A portfolio of US Stocks and US Bonds from 1987-08/31/2019 had a Sharpe ratio of .90 for the Tangency Portfolio, .87 for Risk Parity and .63 for 60/40. Similar comparative results occurred for the FTSE and the Gilt from 1992.

Modern Portfolio theory does allow for randomness - there will always be time frames when Risk Parity does not approach the Tangency portfolio and when 60/40 outperforms - but as long as Sharpe ratios for equities and fixed income remain similar to each other (as they have for at least the last 100 years), Risk Parity will always be the optimal way to allocate between the two asset classes. We hope to persuade investors to focus on this approach before digging deeper into more opaque approaches to improve performance.

**********

Michael Rulle is Founder & CEO of MSR Indices

Contributions by Matthew Brown, President & COO, MSR Indices

***

The views expressed in this article are those of the author and do not necessarily reflect the views of AlphaWeek or its publisher, The Sortino Group